개요
다익스트라(Dijkstra) 알고리즘이란, 그래프의 한 노드에서 모든 노드로의 최단거리를 구하는 알고리즘이다. 주로 간선에 가중치가 매겨져 있는 그래프에서 사용한다. BFS와 비슷하지만, BFS는 모든 노드를 순회하는 것에 초점을 두고 다익스트라 알고리즘은 거리를 구하는 것에 초점을 둔다.
일반적으로 최단 경로 계산에 있어서는 수행 속도가 빠른 알고리즘이지만, 간선의 가중치에 음수가 있다면 사용할 수 없다는 맹점이 있다.
구현
다음과 같은 그래프에서, A로부터 다른 모든 노드들의 최단 거리를 계산하면 옆의 결과가 나온다.
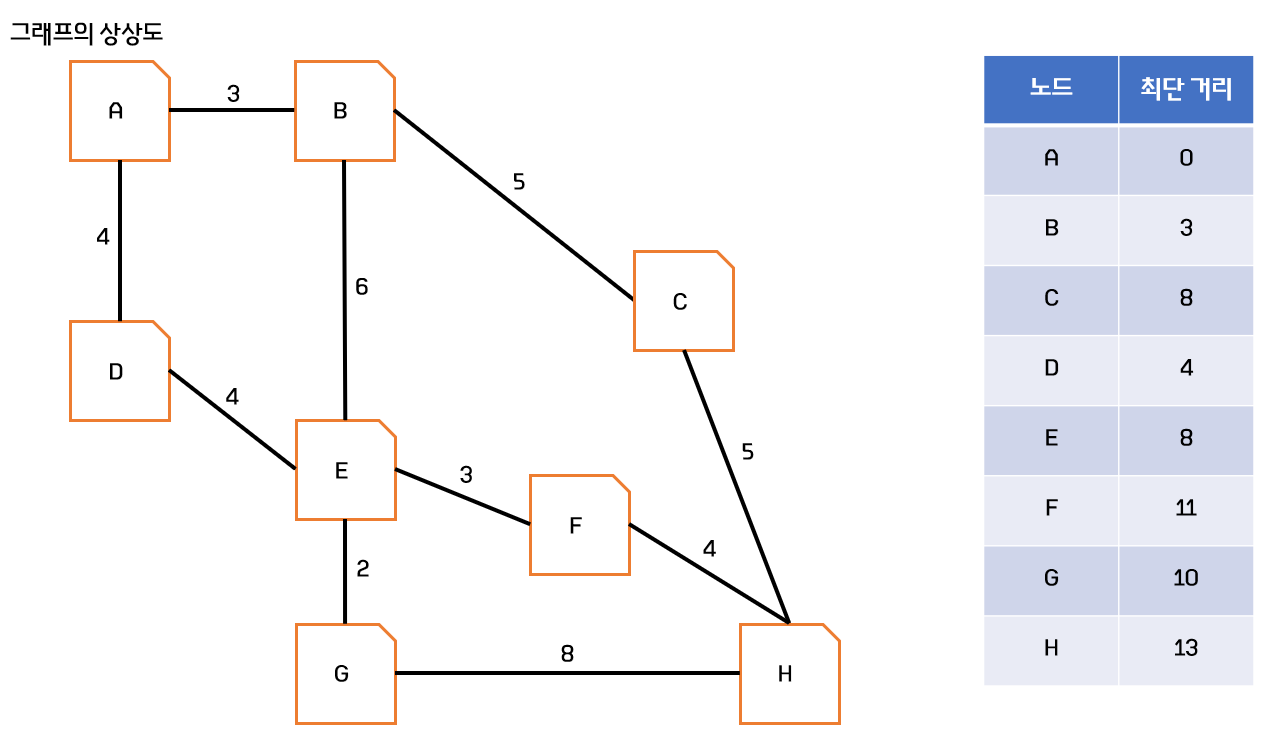
두뇌 CPU를 사용하면 금방 계산이 가능하지만, 현실 CPU는 그리 유연한 사고를 해주지 못한다. 가능한 모든 간선들을 돌면서 가능한 모든 경우의 수를 계산하는 것이다. 그저 A->E까지의 거리를 구하려고 해도, 우리는 '딱 봐도 A-B-E나 A-D-E 둘 중 하나를 비교하면 되겠구나' 하겠지만, 컴퓨터는 'A-B-E, A-D-E, A-B-C-H-F-E, A-B-C-H-G-E...' 이래가면서 비현실적인 수까지 고려하게 된다.
그렇기에 최단 거리를 구하기 위해서는 다음과 같은 것이 필요하다고 볼 수 있다.
1. 각 노드들에 대한 최단 거리를 기록하고, 어떤 경로로 계산해도 가장 작은 값이 유지되도록 할 것
2. 간선들 중 가능한 한 짧은 거리의 노드부터 순회해서 쓸데없는 비용을 최소화 할 것
1번을 위해서는 맵, 배열, 리스트등 전체 노드를 대상으로 하는 아무 자료 구조나 사용하면 된다. 2번의 경우 우선순위 큐를 이용하면 쉽게 가장 짧은 거리를 찾을 수 있다. 준비물도 생각했으니 알고리즘을 세워보자.
1. 최단 거리를 저장할 변수를 D라고 한다.
2. 일단은 시작 노드의 거리값을 D에 저장한다. 자기가 자기를 가리키는 꼴이므로 0이 들어간다.
3. 다른 노드들의 거리값도 저장하는데, 이 땐 가능한 한 가장 큰 수로 지정한다. Integer.MAX_VALUE 등이 해당된다. 이렇게 하는 이유는 앞으로 도출될 최단 거리의 값을 가늠하기 어렵기 때문이다.
4. 현재 노드를 가리킬 A라는 변수에 시작 노드를 대입한다.
5. A와 인접한 노드들(위의 경우 A와 인접한 노드 B,D를 순회)을 대상으로 다음 작업을 수행한다.
5-1. 현재 노드 A와 인접 노드 B 사이의 간선을 P라고 한다.
5-2. [D에 기록된 B의 값(D[B]]과, [D에 기록된 A의 값 + P의 가중치(B[A]+P[A,B]]를 비교해 적은 쪽을 D[B]에 덮어씌운다. 이러면 인접 노드 B까지의 최단 거리가 갱신된다.
6. 순회가 끝나면 A를 방문 처리하고, 인접한 노드들 중 방문한 적이 없으면서 가장 가까운 노드(이걸 우선순위 큐로 저장)를 A에 대입한다.
7. 모든 노드가 방문 처리될 때까지 5~6을 반복한다.
7-1. 만약 도착 노드가 지정되어 있다면, 도착 노드가 방문 처리될 때까지만 반복한다.
뭐가 이렇게... 어렵지...? 싶지만 천천히 톺아보면 알 수 있을지도 모르겠다. 일단 나는 노드와 간선을 다음과 같이 정의했다.

다익스트라 알고리즘은 다음과 같이 정의했다.

...당연히 최선의 코드는 아니지만, 아무튼 다음과 같이 의도대로 작동했다.

어떤 때에 쓰이나
위에서도 설명했듯, 가장 짧은 거리를 알아내고자 할 때 가장 유용하게 쓰인다. 정점의 수를 V, 간선의 수를 E라고 했을 때, 다익스트라 알고리즘의 시간복잡도는 O((V+E)logV)에 수렴한다. 우선순위 큐를 사용하지 않고 무작정 순회하는 경우 O(V^2)까지 늘어난다(DFS, BFS와 같다). BFS는 탐색에 더 유리하고, 다익스트라는 경로 계산에 더 유리하다.
노드의 수보다 간선의 수가 적을수록, 그래프 자체의 규모가 작을수록 다익스트라 알고리즘이 다른 최단 경로 알고리즘들보다 빠르게 작동할 수 있다. 간선이 많아지면 수행시간이 제곱에 비례하게 되고, 그래프의 규모가 커지면 최단 경로를 저장해 둘 공간에 문제가 발생할 수 있기 때문이다.
아래로는 이번 요약에 쓰인 코드 전문이다.
import java.util.*;
record Edge(Vertex vertex, int weight) {}
class Vertex {
private String name;
private PriorityQueue<Edge> edges; // 간선을 저장할 곳
public Vertex(String name) {
this.name = name;
// 오름차순 정렬하여 낮은 값이 먼저 오도록 한다
edges = new PriorityQueue<>((a, b) -> b.weight() - a.weight());
}
public PriorityQueue<Edge> getEdges() {
return edges;
}
public void addEdge(Vertex node, int weight) {
edges.offer(new Edge(node, weight));
}
@Override
public String toString() {
return "<" + name + ">";
}
}
public class Test3 {
public static void main(String[] args) {
Vertex a = new Vertex("A");
Vertex b = new Vertex("B");
Vertex c = new Vertex("C");
Vertex d = new Vertex("D");
Vertex e = new Vertex("E");
Vertex f = new Vertex("F");
Vertex g = new Vertex("G");
Vertex h = new Vertex("H");
a.addEdge(b, 3); a.addEdge(d, 4);
b.addEdge(a, 3); b.addEdge(e, 6); b.addEdge(c, 5);
c.addEdge(b, 5); c.addEdge(h, 5);
d.addEdge(a, 4); d.addEdge(e, 4);
e.addEdge(b, 6); e.addEdge(d, 4); e.addEdge(g, 2); e.addEdge(f, 3);
f.addEdge(e, 3); f.addEdge(h, 4);
g.addEdge(e, 2); g.addEdge(h, 8);
h.addEdge(g, 8); h.addEdge(c, 5);
System.out.println("A 노드에서 다른 노드로 가는 최단 거리는 각각...");
Map<Vertex, Integer> map = dijkstra(a);
for (Entry<Vertex, Integer> entry : map.entrySet()) {
System.out.println(entry.getKey() + " -> " + entry.getValue());
}
}
public static Map<Vertex, Integer> dijkstra(Vertex start) {
Map<Vertex, Integer> distances = new HashMap<Vertex, Integer>();
Set<Vertex> visited = new HashSet<Vertex>();
// 시작 노드에 대한 거리값을 정의한다
distances.put(start, 0);
Vertex curVtx = start;
while (true) {
for (Edge edge : curVtx.getEdges()) {
// 현재 노드까지의 최단 거리 + 현재 노드와 인접 노드간의 거리
int vertexDist = distances.getOrDefault(curVtx, Integer.MAX_VALUE) + edge.weight();
// 인접 노드까지의 최단 거리
int savedDist = distances.getOrDefault(edge.vertex(), Integer.MAX_VALUE);
if (vertexDist < savedDist) {
distances.put(edge.vertex(), vertexDist);
}
}
// 현재 노드를 방문 처리
visited.add(curVtx);
// 가장 가깝고, 방문한 적이 없는 노드를 찾는다
boolean searched = false;
while (!curVtx.getEdges().isEmpty()) {
curVtx = curVtx.getEdges().poll().vertex();
if (!visited.contains(curVtx)) {
searched = true;
break;
}
}
if (!searched)
break;
}
return distances;
}
}'프로그래밍 > 개념원리' 카테고리의 다른 글
| 비트(Bit) (0) | 2024.03.17 |
|---|---|
| 컴퓨터의 3요소 (0) | 2024.03.17 |
| 그래프 - DFS & BFS (0) | 2024.03.12 |
| Heap (0) | 2024.02.25 |
| Linked List (0) | 2024.02.25 |
